우선순위 큐와 힙

1. 우선순위 큐란 

 

> 데이터가 삽입된 순서와 상관없이 우선순위가 높은 데이터가 먼저 나온다.

> 데이터의 우선순위는 우선순위 큐를 구현하면서 임의로 설정하도록 한다.

> 우선순위 큐는 배열, 연결리스트, 힙(heap)등을 이용하여 구현할 수 있는데 일반적으로 힙을 이용한다.

 

2. 힙

 

>  완전 이진 트리이다.

>  부모노드와 자식노드간 대소관계가 있다.

> 이진탐색트리와 달리 중복 값을 허용한다.

 

 

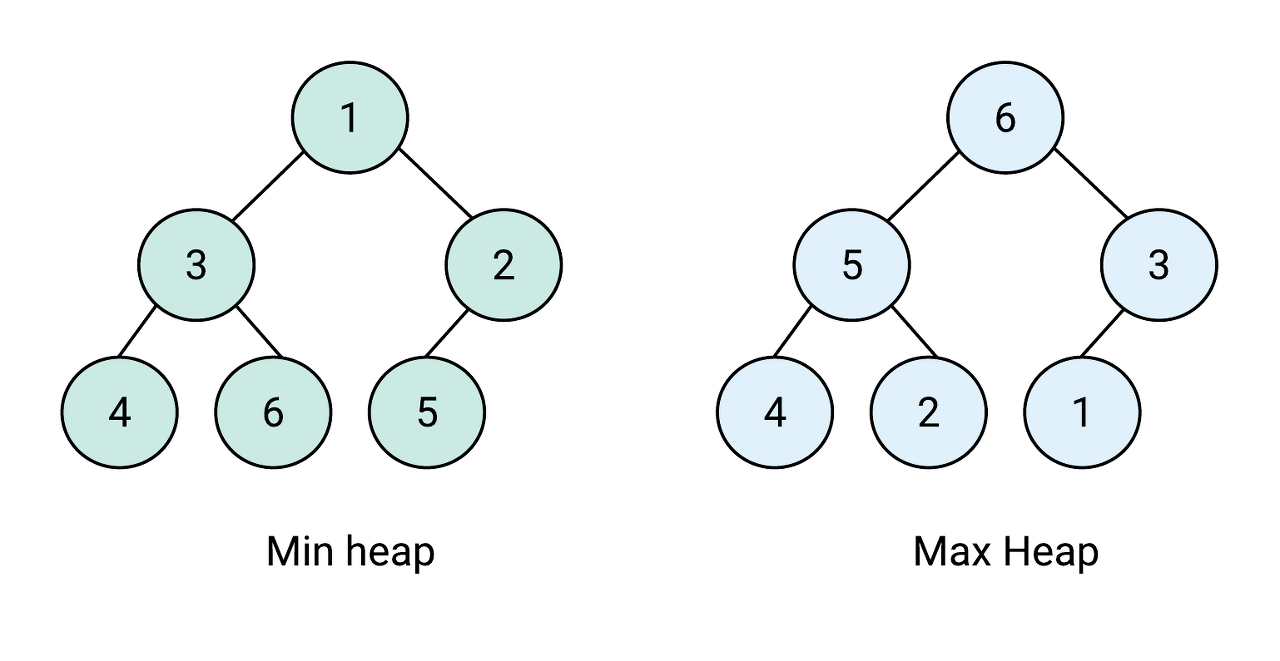
출처:https://passwd.tistory.com/entry/%EC%B5%9C%EC%86%8C%ED%9E%99-%EC%B5%9C%EB%8C%80-%ED%9E%99

최대힙 :루트노드로 올라갈수록 저장된 값이 커지는 완전 이진 트리를 말한다. 

최소힙: 루트노드로 올라갈수록 저장된 값이 작아지는 완전 이진 트리를 말한다.

 

3. 힙의 구현 및 우선순위 큐 완성

 

- 힙의 데이터 저장:  새로운 데이터는 우선순위가 제일 낮다는 가정하에 마지막 위치에 저장

                                적절한 위치를 찾을 때 까지 부모노드와 비교하며 위치를 수정한다.

 

- 힙의 데이터 삭제 : 우선 순위가 가장 높은 root부터 삭제. 

                                 맨 마지막 데이터를 root로 옮김

                                 적절한 위치를 찾을 때 까지 자식노드와 비교한다.

 

우선순위 큐를 구현할 수 있는 배열, 힙, 연결리스트의 삽입 삭제과정의 빅오는 다음과 같다.

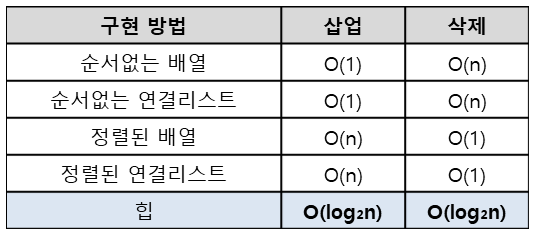
출처: https://suyeon96.tistory.com/31

log2N  -> 데이터 추가(1)+부모노드와 자식노드 사이 비교(높이에 해당하는 숫자만큼 연산)

           ->  이진트리 높이당 늘어나는 최대 데이터 수가 2^K =N  여기서 K는 높이

           ->  따라서주어진 데이터의 수에 따른 연산 횟수는 log2N

 

3.1 배열을 통한 힙의 구현 

 

힙은 완전 이진 트리이지만, 연결리스트가 아닌 배열을 통해 구현한다. 

연결리스트를 기반으로 힙을 구현하면, 새로운 노드를 힙의 마지막에 추가하는 것이 쉽지 않기 때문이다.

 

배열을 기반으로 트리를 구성할 경우 노드에 고유 번호를 부여하고 그 번호가 각 노드에 데이터가 저장 될 배열의 인덱스 값이 된다.

배열의 경우 새로운 노드를 힙의 마지막에 추가하기 위해서 마지막에 저장된 배열의 인덱스만 알면 되므로 매우 간편하다.

 

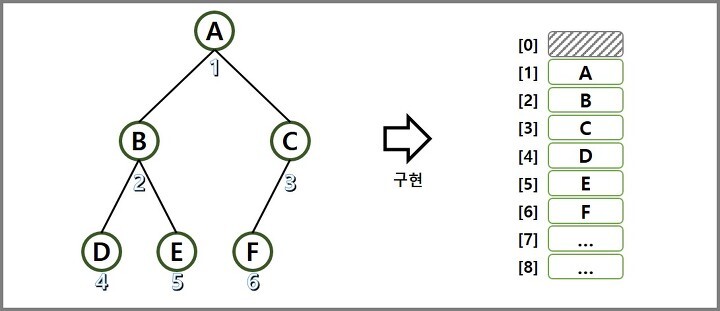
출처:https://yahma.tistory.com/19

 > 왼쪽 자식 노드의 인덱스 값 = 부모 노드의 인덱스 값 *2 

> 오른쪽 자식 노드의 인덱스 값 = 부모 노드의 인덱스 값*2 +1

> 부모 노드의 인덱스 값 = 자식 노드의 인덱스 값%2 

 

4. Simple Heap

 

헤더

#ifndef __SIMPLE_HEAP_H

#define __SIMPLE_HEAP_

#define MAX_LEN 100

typedef char Hdata;

typedef int Priority;

typedef struct _Helem{

    Hdata data;

    Priority pr;

}helem;

typedef struct _Sheep{

    int numofdata;

    helem helemarr[MAX_LEN];

}Heap;

void HeapInit(Heap* hp);

int HisEmpty(Heap* hp);

void HInsert(Heap* hp, Hdata data,Priority pr);

Hdata HDelete(Heap* hp);

#endif

소스

#include "SimpleHeap.h"

void HeapInit(Heap* hp){

    hp->numofdata =0;

}

int HisEmpty(Heap* hp){

    if(hp->numofdata ==0) return 1;

    else return 0;

}

void HInsert(Heap* hp, Hdata data,Priority pr){

    int lastIndex = hp->numofdata +1;

    helem hem = {data,pr};

    int Parent = GetParentIndex(lastIndex);

   

    while(lastIndex != 1){

        if(pr < hp->helemarr[Parent].pr){

             //새로 들어오는 데이터의 우선순위가 Parent의 우선순위보다 높다면

             hp->helemarr[lastIndex] = hp->helemarr[Parent];

             //마지막 자리에 부모노드를 옮김

             lastIndex = Parent; // 이제 새로운 데이터가 들어갈 수 있는 마지막 자리는 부모노드의 고유번호

             Parent = GetParentIndex(lastIndex); // 새로운 부모노드

        }else break; //새로 들어오는 데이터의 우선순위가 Parent와 같거나 낮다면그만! 

    }

   

    hp->helemarr[lastIndex] =hem;

    hp->numofdata +=1;

}

Hdata HDelete(Heap* hp){

    Hdata Ddata = hp->helemarr[1].data;

    helem lastElem = hp->helemarr[hp->numofdata];

   

   

    int Parentnode =1; //빈 부모자리 (지금은 1번)

    int Childnode; // 1번자리두고 마지막 노드랑 경쟁할 우선순위 큰 자식노드  

    while(Childnode = GetTopPriorityChildIndex(hp,Parentnode)){

        if(lastElem.pr <= hp->helemarr[Childnode].pr) //last의 우선순위가 더 크거나 같다면 그만! 

        break;

        else{

            hp->helemarr[Parentnode] = hp->helemarr[Childnode];

            Childnode = Parentnode;

        }

    }

    hp->helemarr[Parentnode] = lastElem;

    hp->numofdata--;

    return Ddata;

}

int GetParentIndex(int idx){

    return idx/2;

}

int GetLeftChildIndex(int idx){

    return idx*2;

}

int GetRightChildIndex(int idx){

        return idx*2+1;

}

int GetTopPriorityChildIndex(Heap* hp,int Parentidx){ //좌 우 자식중 우선순위 높은 노드의 고유번호 return

    //idx는 우선순위에 중복이 없고 순차적 변화라면, 우선순위될 수 있음

    //아니라면, 우선순위에 따라 정렬된 노드의 고유번호

    //여기서는 자식을 비교하고싶은 부모의 고유번호 매개변수로 받음

    //다만 힙의 성질에 의해(완전이진트리) idx로 자식노드가 있는지 하나인지는 판단 가능

    //마지막 인덱스 == 마지막 노드의 고유번호 && 마지막 고유번호 == 저장된 노드의 수

    if(GetLeftChildIndex(Parentidx) > hp->numofdata)

    return 0;

    else if(GetLeftChildIndex(Parentidx) == hp->numofdata)

    return GetLeftChildIndex(Parentidx);

    if(hp->helemarr[GetLeftChildIndex(Parentidx)].pr > hp->helemarr[GetRightChildIndex(Parentidx)].pr)

        return GetRightChildIndex(Parentidx);

    else

        return GetLeftChildIndex(Parentidx);    

   

}

힙을 구현하면서 생각해야할 점 

> 힙은 완전 이진 트리이다.

> 힙의 구현은 배열을 기반으로 하며 인덱스가 0인 요소는 비워둔다.

> 힙에 저장된 노드의 개수와 마지막 노드의 고유번호는 일치한다.

> 노드의 고유번호가 노드가 저장되는 배열의 인덱스 값이 된다.

> 우선순위를 나타내는 정수 값이 작을수록 높은 우선순위를 나타낸다고 가정한다.

 

*고유번호는 데이터를 우선순위별로 정렬할 시 노드가 가지게되는 번호임.  

 

4.1 우선순위가 높은 자식 노드를 얻는 메서드 

 

 GetTopPriorityChildIndex(Heap* hp,int Parentidx)

부모노드의 인덱스를 전달하면

1.자식노드가 있는지 검사 2. 자식노드가 하나인지 검사, 3 왼쪽 - 오른쪽 자식노드 우선순위 큰 자식노드의 인덱스 반환

을 순차적으로 진행한다.

먼저 자식노드가 있는지에 대한 검사식은

if(GetLeftChildIndex(Parentidx) > hp->numofdata)

힙에 저장된 노드의 개수 == 마지막 노드의 고유번호이므로,

만약 자식노드의 인덱스가 저장된 노드의 수보다 많다면, 해당 부모노드는 자식이 없다.

else if(GetLeftChildIndex(Parentidx) == hp->numofdata)

자식노드가 한개라면 저장된 노드의 수와 일치할 것이다.

 

위 두 검사식은 힙이 완전 이진 트리라는 특성을 가진것을 이용한 것이다.

완전 이진 트리가 되기 위해서는 데이터는 항상 순차적으로 위->아래, 왼->오 의 순서를 지켜야한다.

따라서 왼쪽노드만 가진 부모노드는 모든 트리 내에서 1개 혹은 0개이다. 

 

4.2 문제점 

 위에서 구현한 힙은 heapElem에서 볼 수 있듯이 우선순위를 저장하고 있는데, 이러한 우선순위를 데이터에 따라 프로그램이 판단하는게 아니라 insert를 호출하면서 직접 넣어줘야한다.

 

 

5 개선된 Heap

 

heap을 정의하는 구조체를 다음과 같은 형식으로 바꾸려한다

typedef struct _UHeap{
    GetPriority* comp;
    Hdata HeapArr[MAX_LEN]; 
    int numofdata;
}Heap;

이전과 다르게 Helem을 따로 정의하지 않고, Hdata형 배열을 구조체 멤버로 정의하고, 

데이터간 우선순위를 비교할 수 있도록하는 함수의 포인터 멤버를 정의해 두었다.

 

헤더

#ifndef __HEAP_H
#define __HEAP_H

#define MAX_LEN 100

typedef char Hdata;
typedef int GetPriority(Hdata d1, Hdata d2);
//int (*GetPriority)()와 다른점은 *를 빼고 typedef를 선언하면, 
//해당 함수형 포인터를 선언(멤버,변수)할때 *를 꼭 붙여야한다.


typedef struct _UHeap{
    GetPriority* comp;
    Hdata HeapArr[MAX_LEN];
    int numofdata;
}Heap;

void HeapInit(Heap* hp, GetPriority comp);
int HisEmpty(Heap* hp);
void HInsert(Heap* hp, Hdata data);
Hdata HDelete(Heap* hp);


#endif

소스

#include "Heap.h"


void HeapInit(Heap* hp, GetPriority comp){

    hp->numofdata == 0;
    hp->comp = comp;

}
int HisEmpty(Heap* hp){

    if(hp->numofdata ==0) return 1;
    else return 0;

}
void HInsert(Heap* hp, Hdata data){
    int lastIndex = hp->numofdata +1;
   
    while(lastIndex != 1){
        if(hp->comp(data,hp->HeapArr[GetParentIndex(lastIndex)]) > 0){
        hp->HeapArr[lastIndex] = hp->HeapArr[GetParentIndex(lastIndex)];
        lastIndex = GetParentIndex(lastIndex);
        }
        else break;
    }
    hp->HeapArr[lastIndex] = data;
    hp->numofdata += 1;

}
Hdata HDelete(Heap* hp){
    Hdata Ddata = hp->HeapArr[1];
    Hdata lastdata = hp->HeapArr[hp->numofdata];

    int Parentidx = 1;
    int Childidx;

    while( Childidx = GetTopPriorityChildIndex(hp,Parentidx)){
        if(hp->comp(lastdata,hp->HeapArr[Childidx])>=0)
        break;

        hp->HeapArr[Parentidx] = hp->HeapArr[Childidx];
        Parentidx = Childidx;
    }
    hp->HeapArr[Parentidx] = lastdata;
    hp->numofdata -=1;
    return Ddata;

}

int GetLeftChildIndex(int idx){ return idx*2;}
int GetRightChildIndex(int idx){ return idx*2+1;}
int GetParentIndex(int idx){return idx/2;}

int GetTopPriorityChildIndex(Heap* hp, int idx){

    if(GetLeftChildIndex(idx) > hp->numofdata)
    return 0;
    else if(GetLeftChildIndex(idx) == hp->numofdata)
    return GetLeftChildIndex(idx);

    if(hp->comp(hp->HeapArr[GetLeftChildIndex(idx)],hp->HeapArr[GetRightChildIndex(idx)])<0)
     return GetRightChildIndex(idx);
     else return GetLeftChildIndex(idx);

}

전체적으로 코드가 많이 수정된 것은 아니고, 우선순위를 비교하는 부분만 hp의 함수를 호출해서 simple heap에서 직접 우선순위멤버를 비교한 것이 아니라, 데이터별 우선순위를 정해진 규칙에 따라 비교하도록 수정해두었다.

 

int DataPriorityComp(char n1, char n2) //비교에 사용될 함수
{
	return ch2-ch1;
}
//우선순위 같으면 0, 왼쪽이 높으면 양수, 오른쪽이 높으면 음수 (오름차순)

 

6. 우선순위 큐의 ADT 및 구현 

 

void PQueueInit(PQueue* ppq, GetPriority pc);
우선순위 큐 초기화, 우선순위 큐 생성 후 제일 먼저 호출
int PQisEmpty(PQueue* ppq);
우선순위 큐가 빈 경우 1 아니면 0 반환

void PEnqueue(PQueue * ppq, PQdata data);
전달된 데이터 저장
PQdata PDqueue(PQueue* ppq);
우선순위 가장 높은 데이터 삭제후 삭제된 데이터 반환 
본 함수의 호출을 위해서는 데이터가 하나 이상 존재함이 보장되어야함

헤더

#ifndef __PRIORITY_QUEUE_H
#define __PRIORITY_QUEUE_H

#include "Heap.h"

typedef Heap PQueue;
typedef Hdata PQdata;

void PQueueInit(PQueue* ppq, GetPriority pc);
int PQisEmpty(PQueue* ppq);

void PEnqueue(PQueue * ppq, PQdata data);
PQdata PDqueue(PQueue* ppq);

#endif

소스

#include "PriorityQueue.h"
#include "Heap.h"

void PQueueInit(PQueue* ppq, GetPriority pc){
    HeapInit(ppq,pc);
}
int PQisEmpty(PQueue* ppq){
    return HisEmpty(ppq);
}

void PEnqueue(PQueue * ppq, PQdata data){
    HInsert(ppq,data);
}
PQdata PDqueue(PQueue* ppq){
    return HDelete(ppq);
}

 

 

참고자료:

윤성우 열혈자료구조

 https://suyeon96.tistory.com/31