-
Tree - 이진 트리의 구현과 순회자료구조와 알고리즘/자료구조 2023. 5. 15. 22:48
1. 배열? 연결리스트?
이진트리는 배열로 구현할 수도 있고 연결리스트로 구현할 수 도 있다. 이때 트리가 완성 된 후 빈번한 탐색이 이루어지는 등 특정한 필요에 따라 배열로 구현할 수 있지만 (ex heap) 일단 연결리스트로 구현해 보자.
2. 이진 트리의 ADT
BTreeNode* MakeBTreeNode(void) - 이진 트리 노드를 생성하여 그 주소 값을 반환
BTdata GetData(BtreeNode*bt) - 노드에 저장된 데이터를 반환
void SetData(BTreeNode*bt, BTdata data) - 노드에 데이터를 저장함
BTreeNode* GetLeftSubTree(BTreeNode* bt) - 왼쪽 서브트리의 주소를 반환
BTreeNode* GetRightSubTree(BTreeNode* bt) - 오른쪽 서브트리 주소를 반환
void MakeLeftSubTree(BTreeNode * main, BTreeNode* sub) - 왼쪽 서브트리를 연결
void MakeRightsubTree(BTreeNode* main, BTreeNode*sub) - 오른쪽 서브트리를 연결
3. 구현 (순회 포함)
헤더
#ifndef __BTree_H#define __BTree_H
typedef int BTdata;
typedef void VisitFuncPtr(BTdata data);
typedef struct _btreeNode{BTdata data;struct _btreeNode* left;struct _btreeNode* right;}BTreeNode;
BTreeNode* MakeBTreeNode(void);BTdata GetData(BTreeNode* bt);void SetData(BTreeNode* bt, BTdata data);BTreeNode* GetLeftSubTree(BTreeNode* bt);BTreeNode* GetRightSubTree(BTreeNode* bt);void MakeLeftSubTree(BTreeNode* main, BTreeNode* sub);void MakeRightSubTree(BTreeNode* main, BTreeNode* sub);void PreorderTraverse(BTreeNode* bt,VisitFuncPtr action);void PostorderTraverse(BTreeNode* bt,VisitFuncPtr action);void InorderTraverse(BTreeNode* bt,VisitFuncPtr action);
#endif소스
#include<stdlib.h>#include"BTree.h"
BTreeNode* MakeBTreeNode(void){BTreeNode* new = (BTreeNode*)malloc(sizeof(BTreeNode));new->left = NULL;new->right = NULL;return new;}BTdata GetData(BTreeNode* bt){return bt->data;}void SetData(BTreeNode* bt, BTdata data){bt->data = data;}BTreeNode* GetLeftSubTree(BTreeNode* bt){return bt->left;}BTreeNode* GetRightSubTree(BTreeNode* bt){return bt->right;
}void MakeLeftSubTree(BTreeNode* main, BTreeNode* sub){if(main->left != NULL){ //순회 필요함free(main->left);//Delete(main->left); 왼쪽 서브트리 모두 삭제}main->left = sub;
}void MakeRightSubTree(BTreeNode* main, BTreeNode* sub){
if(main->right != NULL){free(main->right);//Delete(main->right); 오른쪽 서브트리 모두 삭제}main->right = sub;}
void InorderTraverse(BTreeNode* bt,VisitFuncPtr action){if(bt == NULL) return;InorderTraverse(bt->left,action);action(bt->data);InorderTraverse(bt->right,action);}void PreorderTraverse(BTreeNode* bt,VisitFuncPtr action){if(bt == NULL) return;action(bt->data);PreorderTraverse(bt->left,action);PreorderTraverse(bt->right,action);}void PostorderTraverse(BTreeNode* bt,VisitFuncPtr action){if(bt == NULL) return;PostorderTraverse(bt->left,action);PostorderTraverse(bt->right,action);action(bt->data);}void DeleteTree(BTreeNode * bt){if(bt == NULL) return;
DeleteTree(bt->left);DeleteTree(bt->right);free(bt);}> 왜 이진트리의 구조체는 없는가?
헤더 파일을 보면, 구조체로 노드만 선언되어 있고, 이진트리의 구조체는 선언되어 있지 않음을 볼 수 있다.
앞 서 선형 자료구조에서 노드와 연결리스트의 구조체를 각각 선언한 것과 차이가 보인다.
이러한 헤더 파일을 통해 비선형 자료구조와 선형 자료구조의 차이점을 볼 수 있다.
-선형 자료구조는 데이터를 저장하고, 삭제하는 등의 기능을 통해 표현하려는 것이 일관된다
(물론 저장과 삭제의 방향은 다를 수 있다.)
*미리 완성된 자료구조에 기능만을 사용하는 측면이 있다.
- 비선형 자료구조는 무엇을 표현하느냐에 따라 트리를 다르게 구성할 수 있음으로, 하나의 이진트리를 구조체로 선언한들 이를 모든 표현에 사용할 수 없음으로, 따로 이진트리의 구조체를 선언하는 대신에 이진 트리를 만들 수 있는 도구들을 선언해 둔 것이다.
즉 위 헤더파일은 이진트리를 만드는 도구이지 완성된 이진트리 자체가 아니다!
> 왜 노드 앞에 Tree라는 이름을 붙였는가?
이는 트리에서 노드는 노드이자 하나의 트리이기 때문이다. 하나의 노드에도 공집합 노드가 달려있음으로 노드의 관점과 트리의 관점을 모두 가져간다.
4. 이진 트리의 순회(Traversal)
이진트리에서 순회가 필요한 이유는 트리에 노드를 삭제하는 과정이나, 트리에 모든 노드의 데이터를 출력하는 등
트리에 모든 노드에 접근해야할 때가 있기 때문이다.
4.1 순회의 종류
- 전위 순회 -> 루트 노드 먼저
- 중위 순회 -> 루트 노드를 중간에
- 후위 순회 -> 루트 노드를 마지막에
모든 순회는 재귀적으로 구현되므로 순회를 마무리할 종료조건이 필요하다.
리프 노드까지는 방문하고 공집합의 노드일 때 순회를 마무리하면 되므로, BTreeNode* temp == NULL 일때 순회를 종료하면 될 것이다.
> 전위 순회
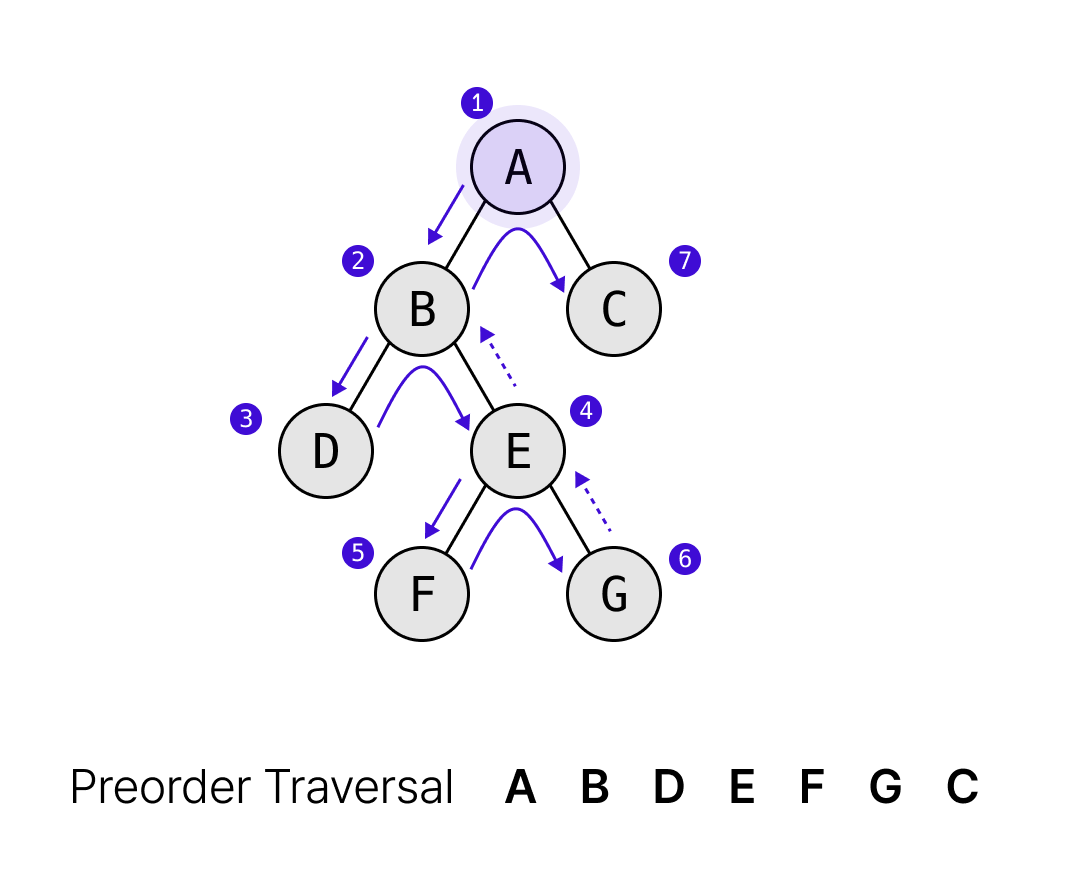
출처:https://www.jiwon.me/binary-tree-traversal/ void PreorderTraverse(BTreeNode* bt,VisitFuncPtr action){if(bt == NULL) return;action(bt->data);PreorderTraverse(bt->left,action);PreorderTraverse(bt->right,action);}루트 노드부터 방문하여 데이터를 적절히 처리하고 왼쪽 -> 오른쪽으로 뻗어나가는 순회이다.
> 중위 순회
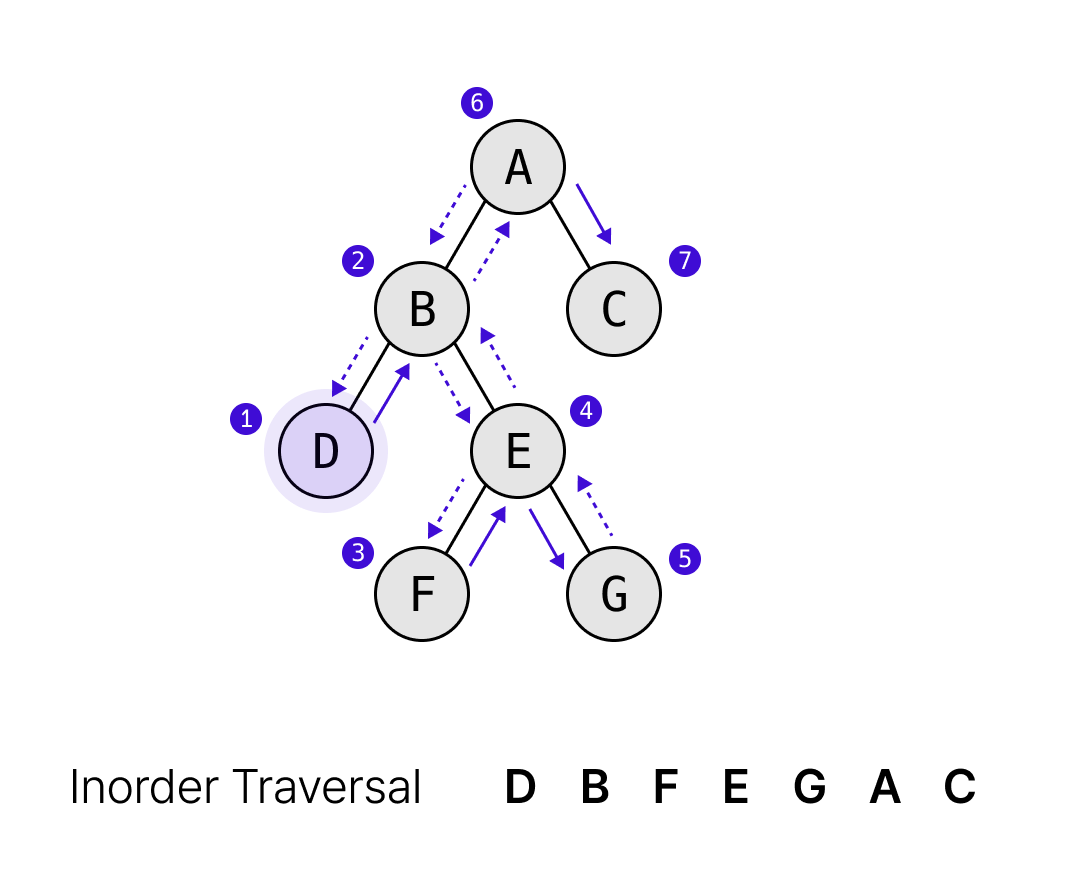
출처:https://www.jiwon.me/binary-tree-traversal/ void InorderTraverse(BTreeNode* bt,VisitFuncPtr action){if(bt == NULL) return;InorderTraverse(bt->left,action);action(bt->data);InorderTraverse(bt->right,action);}가장 왼쪽노드 -> 루트노드 -> 오른쪽 노드 순서로 순회한다.
> 후위 순회

출처: https://www.jiwon.me/binary-tree-traversal/ void PostorderTraverse(BTreeNode* bt,VisitFuncPtr action){if(bt == NULL) return;PostorderTraverse(bt->left,action);PostorderTraverse(bt->right,action);action(bt->data);}왼쪽 -> 오른쪽 -> 루트 노드의 순서로 순회한다.
재귀 함수의 순서만 적절히 배치해주면 된다.
* VisitFuncPtr 각 노드에 데이터에 접근해서 적절한 처리를 하기 위한 함수형 포인터
typedef void VisitFuncPtr(BTdata data);대입될 함수는 외부에서 주어진다.
ex void ShowData(int data) -- if BTdata == int
{ printf("%d ", data); }
void DeleteTree(BTreeNode * bt){if(bt == NULL) return;
DeleteTree(bt->left);DeleteTree(bt->right);free(bt);}후위 순회를 통해 서브트리 모두 제거
> 후위인 이유는 루프노드가 가장 마지막에 제거되야함 중간에 제거되면 루트노드를 통해 왼쪽 오른쪽 노드로 순회할 수 없음
참고자료: 윤성우 열혈자료구조
'자료구조와 알고리즘 > 자료구조' 카테고리의 다른 글
우선순위 큐와 힙 (0) 2023.05.18 Tree - 수식 트리 (Expression Tree) (0) 2023.05.16 Tree - 트리와 이진트리란 (0) 2023.05.15 Deque (0) 2023.05.14 Queue - 원형 큐, 연결리스트 (0) 2023.05.13